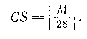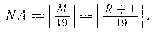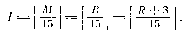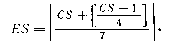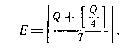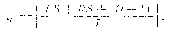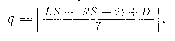| 2013-06-22, 3:26 AM | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
По-видимому, из-за того, что при написании чисел римскими цифрами очень легко допустить ошибку, западноевропейские историки и вычислители («компутисты») разработали целый «набор» разнообразных календарных характеристик, которые широко использовались при датировке документов. Вот три характерных примера. Первый — акт от 15 сентября 1011 г. «от воплощения Господа нашего Ис. Хр.» датирован так: anno ab incarnatione Dom. nostri I. Ch. MXI, indictione IX, littera VII, luna XIV, XVII Kal. Octobr. Далее, грамота из Лионского епископства от 11 марта 1134 г.: Die dominico... V idus Martii, luna decima secunda, anno ab incarn. Dom. millesimo cente-simo trigesimo quarto, indict. VII, epacta XXIII, concurrente VII. И еще одна датировка: a. d. inc. 1223, epacta XXVIII, concurrente VI, indictione XII. Как и на Востоке. Солнечный цикл, золотое число и индикт — эти элементы датировки по своей природе тождественны с теми, которые использовались на христианском Востоке — в Византии и на Руси. Некоторое различие имеется в «точках отсчета» и обозначениях. Как и на Востоке, упомянутые выше циклы сначала отсчитывались в эре от «сотворения мира». По одному из вариантов ее эпоха была отнесена на 4713 г. до н.э. Поэтому число «года мира» М — Annus Mundi находим по формуле M = 4713 + R, где R — номер года н. э. Западноевропейский круг Солнца, точнее «солнечный цикл» (cyclus solaris — CS), определяется как остаток от деления числа «года мира» на 28:
Однако эра года мира в позднем средневековье практически не использовалась, так как Западная Европа, начиная уже с VII в. довольно быстро перешла на счет лет от «рождества Христова». Поэтому солнечный цикл обычно находился при делении на 28 числа года н. э. R, увеличенного на 9: 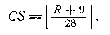 В частности, для 1986 г. имеем CS — 7 (VII). Следовательно, по отношению к восточному кругу Солнца Q западноевропейский солнечный цикл отставал на 11: CS = Q — 11. Золотое число (numerus aureus — AM)— номер года в 19-летнем лунном цикле (cyclus lunaris) определяется в результате деления на 19 года мира М или увеличенного на 1 числа года и. э. R:
Для того же 1986 г. находим NA = 11 (XI). Ранее уже отмечалось, что золотое число года на 3 больше круга Луны: NA = L + 3. Очевидно, что поскольку переход от кругов Солнца Q к западноевропейским солнечным циклам CS и от кругов Луны L к золотым числам NA элементарен, здесь нет необходимости приводить таблицы, по которым они определяются для любого года и столетия. Для этого достаточно взять числа из табл. и сделать соответствующую поправку. Эпоха эры года мира М такова, что числовое значение индикта в Западной и Восточной Европе было одинаковым: Для 1986 г. имеем I= 9 (IX). Проставляя в скобках все характеристики года римскими цифрами, мы напомнили читателю, что именно в таком виде и приводились они на всех документах. Таблица индиктов уже приведена ранее. Воскресные буквы. Дни года, начиная с 1 января и по 31 декабря, средневековые «компутисты» обозначили циклично семью латинскими буквами А, В, С, D, Е, F, G, получившими название календарных букв (litterae calendarum). «Привязка» букв к числам месяцев проведена в прямом порядке: 1 января — А, 2-е — В, 3-е — С, 4-е — D, ..., 8-е — А, 9-е — В и т. д. В итоге на первые числа месяцев приходились следующие буквы: 1 янв. — А, 1 апр. — G, 1 июля —G, 1 окт. —А, 1 февр. — D, 1 мая — В, 1 авг. — С, 1 ноября — D, 1 марта — D, 1 июня — Е, 1 сент. — F, 1 дек. — F. Календарная
буква, на которую в текущем году приходилось воскресенье, получала
название воскресной буквы этого года (littera dominicalis — LD).
Очевидно, что роли воскресных букв и вруцелет тождественны. Однако
вруцелето использовалось в мартовском году, в котором дополнительный,
366 день года вставлялся в самом его конце. Поэтому такая вставка
приводила лишь к тому, что в ряду вруцелет происходил переход на две
(вместо одной) позиции. Так, вруцелето 1983 мартовского юлианского года
было Д, 1984 — S. В календаре же январского стиля високосный год имеет две воскресные буквы. Первая — «очередная» — указывает дату воскресенья от 1 января до 29 февраля, вторая из ряда календарных букв (записанных в обратном порядке: A, G, F, Е, D, С, В, А) —с 1 марта по 31 декабря. Распределение воскресных букв (LD) в 28-летнем солнечном периоде дано в табл. Отметим, что високосными являются 1-й, 5-й и т. д. годы периода, причем 1-й год начинается с понедельника. Для примера определим, на какой день недели пришлось 11 марта 1134 г. Прибавив к числу года 9 и разделив на 28, находим в остатке солнечный цикл CS = 23. Из табл. следует, что воскресная буква 23-го года G, которая в марте приходится на 4, 11, 18 и 25 числа. Следовательно, 11 марта 1134 г.— воскресенье. В средневековых документах часто вместо воскресной буквы указывалось ее порядковое число в ряду календарных букв: A —littera I, В — litters II, С —littera III, D — littera IV, E —littera V, F — littera VI и G — littera VII. Воскресная буква G и «зашифрована» как «littera VII» в акте от 15 сентября 1011 г. Конкурренты. Две из приведенных выше датировок содержат мало известный у нас элемент — конкур-ренту. Между тем конкурренты, или солнечные эпак-ты (concurrentes septimanae, epactae solis — ES) широко использовались начиная с VIII в. для отождествления календарной даты с днем недели. Первым, но отнюдь не главным назначением конкурренты было указать день недели, на который в том или другом году приходилось 24 марта: при конкурренте 1 это воскресенье, 2 — понедельник, 3 — вторник, 4 — среда, 5 — четверг, 6 — пятница и 7 — суббота. Распределение конкуррент по годам солнечного цикла дано в табл. Как видно, между воскресными буквами и конкуррентами имеется однозначная связь: F = 1, Е = 2, D = 3, С = 4,В = 5, А = 6 и G = 7. Это понятно. Если воскресной является, например, буква G, то 24 марта приходится на субботу и т. д. В високосном году для января — февраля следует брать конкурренту, соответствующую первой воскресной букве, т. е. на единицу меньше указанной в таблице. Таблица. Расположение воскресных букв и конкуррент в 28-летнем солнечном цикле
Возьмем к примеру 1340 г. Его солнечный цикл CS — 5. Из табл. видно, что конкуррентой этого года (солнечной эпактой) было число 6 (воскресная буква для марта—декабря — А). Следовательно, 24 марта 1340 г. приходилось на пятницу. Однако основная роль солнечных эпакт (конкуррент) заключается в следующем. Солнечная эпакта — это число, указывающее, на сколько позиций в конкретном году солнечного цикла с номером CS (или Q для византийского счета) день недели, рассчитанный на определенную календарную дату, продвинулся вперед по сравнению с исходным («нулевым») годом цикла. Очевидно, что при расчете солнечных эпакт необходимо принимать во внимание положение високосных годов в 28-летнем солнечном цикле. Как уже отмечалось, в западноевропейском 28-летнем цикле високосными являются 1-й, 5-й, 9-й и т. д. годы. Поэтому с 1 марта 1-го года цикла происходит сдвиг дней недели на две позиции по сравнению с последним годом цикла. Это снова произойдет в 5-м и т. д. годах. Таким образом, солнечную эпакту года, имеющего в 28-летнем цикле номер CS, можно определить по такой несложной формуле:
При этом в январе — феврале високосного года величина ES на единицу меньше, чем это следует из формулы. В византийском 28-летнем цикле високосными являются 3-й, 7-й и т. д. мартовские годы или 4-й, 8-й, 12-й, ... годы январского стиля. Поэтому при расчете солнечных эпакт здесь необходимо использовать несколько другую формулу:
Примечательно, что распределение солнечных эпакт по годам зависит от того, каким циклом пользуется вычислитель. В случае восточного цикла их ряд выглядит так: 1, 2, 3, 5, 6, 7, 1,3,... (как в табл. вруцелет!), в западном цикле имеем 1, 2, 3, 4, 6, 7, 1, 2, 4, ... Это различие обусловлено тем, что начала циклов смещены друг относительно друга (Q = CS+11!) как раз настолько, что на самом деле обоим соответствует единственное распределение солнечных эпакт по годам н. э. Лунные буквы, числа и эпакты. Для определения возраста Луны на конкретную дату в раннем средневековье использовали лунные буквы (litterae lunares). Это 20 букв латинского алфавита от А до U, которые записывались в трех различных вариантах и объединялись в две группы — всего 30 + 29 = 59 — по числу дней соответственно в полном и пустом лунных месяцах. Дни от 1 по 20 января обозначались буквами А, В, С, ,,,, U (их называли litterae nudae), далее проставлялись те же буквы, но со звездочкой: 21 января — А*, 22 —В*, ... (это litterae postpunctatae) и, наконец, со значком перед буквой: 10 февраля — *А, 11 — *В, ... (litterae praepuncta-tae), здесь последняя буква *U не проставлялась. Потом цикл повторялся в том же порядке, так что, в частности, буква А распределялась по месяцам следующим образом: А =1.01; 1.03; 29.04; 27.06; 25.08; 23.10; 21.12; А* = 21.01; 21.03; 19.05; 17.07, 14.09; 12.11; *А= 10.02; 10.04; 8.06; 6.08; 4.10; 2.12. Год заканчивался буквой L = 31 декабря. Следовательно, если каким-то образом было установлено, что в определенном году новолуние приходится, скажем, на 3 января, обозначенное буквой С, то и новолуния всех остальных полных месяцев также приходятся на календарные числа, обозначенные той же буквой. Новолуния же пустых месяцев в 29 дней будут в дни, обозначенные буквой N.. Тем самым устанавливалось расписание фаз Луны на целый год. Особенно эти буквы оказались полезными для обозначения дней с 22 марта (B*) по 25 апреля (*Q), т. е. при расчетах даты пасхи. Использовались для датировки и числа, указывавшие отсчитанный от ближайшего прошедшего новолуния возраст Луны на день пасхи (luna paschae). Например, в составленной Дионисием Малым в 525 г. таблице дат пасхи для года 532 указано luna paschae = XX, так как в указанном году пасха была 11 апреля, а неомения 23 марта. По включительному счету 23 марта — 1-й день, а 11 апреля — 20-й. На протяжении многих веков как для расчетов дат пасхи, так и датировки документов использовались лунные эпакты (epactae lunares, EL) — возраст Луны на 22 марта. О том, как изменяется этот возраст на протяжении 19-летнего цикла, уже говорилось. Там же в табл. и даны лунные эпакты на каждый год цикла. Лунные эпакты обычно указывались в датировках вместо золотого числа года, как это видно из второго и третьего из приведенных выше примеров. Смена эпакт производилась 1 сентября, так что для дат с 1 сентября по 31 декабря указывалась эпакта следующего года. В частности, для 1134 г. находим: золотое число NA — 14 и лунная эпакта EL = XXIII, как и записано в документе. Для 1223 г. NA = 8 и ему соответствует эпакта EL = XVII. В документе, однако, проставлена эпакта XXVIII. Следовательно, он составлен после 1 сентября, что и подтверждается в другом месте. Остается еще выяснить смысл обозначения «luna decima secunda», т. е. «Луна-12» в документе от II марта 1134 г. Это — возраст Луны, указывающий ее фазу на момент составления документа. Из «расписания» новолуний на 19-летний цикл находим, что в 1134 г. при золотом числе года NA = 14 ближайшее прошедшее новолуние было 28 февраля, так что к 11 марта возраст Луны действительно был 12. В 1011 г. (при NA=5) расчетная неомения приходилась на 2 сентября, а к 15 сентября (включительного счета) возраст Луны был 14. Это могло дать повод к ошибочному представлению, будто в последнем случае под «luna XIV» подразумевается лунная эпакта, которая в этом году также равна XIV. Регуляры. Здесь уместно остановиться еще на одних мало известных календарных элементах — регуляpax. Именно они, несомненно, способствовали разработке разнообразных «вечных календарей» с вспомогательными коэффициентами на каждый месяц года. Солнечные регуляры (regulares solares mensium, RS) —это числа, по одному для каждого из месяцев года, которые необходимо прибавлять к конкуррен-там, чтобы получить день недели на 1-е число месяца. Изобрел их, по-видимому, еще в VIII в. церковный историк Беда Достопочтенный. Вот значения этих чисел: Январь — 2, Май —3, Сентябрь — 7, Февраль — 5, Июнь — 6, Октябрь — 2, Март —5, Июль —1, Ноябрь —5, Апрель —1, Август — 4, Декабрь —7. Проверим день недели, приходившийся на 3 мая 1340 г. Солнечный цикл года CS = 5, конкуррента (солнечная эпакта) ES= 6, солнечная регуляра для мая RSV = 3. Следовательно, 1 мая 1340 г. было в 6 + 3 = (9 — 7=) 2—-понедельник, а 3 мая —в среду. Обобщая сказанное, можно для определения числа дня недели q записать такую простую формулу:
Здесь D — число месяца. Оно уменьшается на 1, так как, отдавая дань древнеримской традиции, средневековые вычислители рассчитали регуляры на 1-е .число каждого месяца «включительного счета», т. е. (уже включив его в значение регуляра. Очевидно, что с сегодняшней точки зрения целесообразнее числитель формулы (1.3) переписать так:ES + (RS — 1) + D, т. е. уменьшить на 1 численные значения регуляров. Кроме того, счет дней в неделе в наше время принято начинать с понедельника. Поэтому регуляры Беды Достопочтенного следует уменьшить еще на 1, В итоге формула перепишется так:
Численные значения регуляров определяются из следующих соображений. Пусть 1 января исходного простого года пришлось на среду (q — 3). Если бы все месяцы года имели по 28 дней, то их первые числа приходились бы на тот же день, что и начало года. Но в январе насчитывается 4 полные недели и еще 3 дня, в феврале — 4 недели, в марте — 4 недели и 3 дня, в апреле — 4 недели и 2 дня и т. д. Расписывая дни недели по числам месяцев, замечаем, что к II февраля в их ряду произошел сдвиг на три дня и оно приходится на 3 + 3 = 6-й день, т. е. на субботу, 1 марта — это также суббота. Далее, так как в марте 28 + 3 дня, то 1 апреля придется на 6 + 3 = 9(—7=) = 2 — на вторник, 1 мая — на 2 + 2 = 4 — .четверг и т. д. Поэтому регуляром для января будет .число 2, для февраля 2 + 3 = 5, для марта 5 + 0 = 5, для апреля 5 + 3(—7) = 1 и т. д. Так и составлена приведенная выше табличка. Очевидно, что разности величин регуляров остаются одинаковыми независимо от того, пришлось 1 января на понедельник, среду или субботу: ведь они определяются остатками от деления на 7 числа дней в календарных месяцах. Заметим, что вставку 366-го дня в конце февраля високосного года можно учесть, уменьшив на 1 числа регуляров января и февраля. Тогда формула будет пригодной на протяжении целого календарного года. Из формулы видно, что: а) в каждом определенном календарном году величина конкурренты ES имеет конкретное значение и при переходе от месяца к месяцу изменяется лишь значение регуляра RS; б) при переходе от года к году 28-летнего солнечного цикла величина солнечной эпакты ES изменяется известным образом. Поэтому можно составить месячные коэффициенты К = ES + (RS - 2) для каждого из 12 месяцев определенного года и их табличку для всех годов 28-летнего солнечного цикла. Тогда день недели определится как q = |(K + D)/7| Очевидно, что в юлианском календаре значения месячных коэффициентов К полностью повторяются через каждые 28 лет и через 28*25 = 700 лет. Сопоставив годы 28-летнего цикла с конкретными годами н. э., получаем своеобразный «вечный календарь» с месячными коэффициентами. Лунные регуляры (regulares lunares, RL) дают возможность рассчитать возраст (фазу) Луны на 1-е число календарного месяца в любом году 19-летнего цикла по известным фазам на первые числа месяца в первом году цикла. Эти последние для года с золотым числом NA — 1 расписываются так: 1 января —9, 1мая —11, 1 сентября—16, 1 февраля — 10, 1июня —12, 1 октября —16, 1 марта —9, 1 июля —13, 1 ноября —18, 1 апреля — 10, 1августа — 14, 1 декабря — 18. Для установления возраста Луны на 1-е число любого года 19-летнего цикла достаточно к лунному регуляру месяца прибавить лунную эпакту данного года и вычесть, если нужно, 30. Для примера установим возраст Луны на 1 августа 1370 г. Золотое число года NA = 3. Из табл. 9 находим лунную эпакту EL = XXII. Следовательно, искомый возраст Луны равен 22 + 14 = (36 — 30 =) 6 дней (включительного счета!), так что новолуние (точнее кеомения) в 1370 г. было 27 июля. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 1075 | Загрузок: 0 | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |